Método de Montante
Este método a diferencia del método Gauss Jordán presenta la ventaja de que si al iniciar la solución de cualquier Matriz ó Determinante este solo tiene Números Enteros se trabajará solamente con números enteros y no da lugar a la aparición de elementos fraccionarios facilitando el procedimiento en él calculo manual. El método Montante originalmente se llamó “ Algoritmo Montante” porque desde el punto de vista matemático es un algoritmo pero desde el punto de vista numérico es un método.
Algoritmo Montante
El algoritmo Montante se basa en hacer transformaciones de los elementos de los Determinantes o de las Matrices, para transformarlos a Determinantes o Matrices equivalentes.
Dichas transformaciones “giran” sobre un elemento llamado “Pivote” ( P) el cual puede estar en cualquier Fila ( renglón ) o Columna. La formula Montante para las transformaciones de los elementos es la siguiente:

En donde.
N.E. Nuevo Elemento (o elemento transformado)
P. Pivote
E.A. Elemento Actual (o elemento a transformar)
E.C.F.P. Elemento Correspondiente a la Fila del Pivote
E.C.C.P. Elemento Correspondiente a la Columna del pivote
P.A. Pivote Anterior
Algoritmo montante aplicado a la solución de determinantes
A continuación se detallarán algunos pasos que nos servirán para encontrar la solución de Determinantes
- Cualquier elemento puede ser tomado como “Pivote”, excepto los elementos “cero”, (a menos de que sea la última transformación).
- Se escoge el Pivote, se Aísla la Fila y la Columna del Pivote
- En la primera transformación el “Pivote Anterior” toma el valor de uno.
- Los elementos de fila y columna del elemento pivote intervienen solamente para los cálculos, correspondiendo a los elementos restantes las transformaciones por la aplicación de la fórmula Montante.
- A cada transformación le corresponde un signo Positivo o Negativo según sea el signo del cofactor del Pivote.
- Todo número que se multiplique por el Pivote se le considerará Diagonal Principal.
Ejemplo 1
Calcular el siguiente Determinante de orden 2×2
Cualquiera de los cuatro elementos puede ser “Pivote” trataremos siempre que el Pivote sea el primer elemento ( 3 ) como “Pivote”
Solución

Ejemplo 2
Calcular el siguiente Determinante de orden 3×3

Solución

Explicando las 4 operaciones iniciales de la formula Montante que son:

NOTA. Si al dividir entre el Pivote Anterior en el Método Montante, aparece una cantidad fraccionaria, esto será una señal de que se cometió un error, esta es una de las ventajas que tiene el utilizar el Método Montante (las divisiones entre el Pivote Anterior siempre son exactas).
Ejemplo 3
Calcular el siguiente determinante de orden 4×5

Solución

Nota: Los pasos del desarrollo se dejan para el Estudiante.
Algoritmo montante aplicado a la solución de sistemas de ecuaciones lineales
El Algoritmo Montante también es aplicado en la solución de Sistemas de Ecuaciones Lineales con coeficientes enteros, por lo que debemos de tener cuidado de que si alguna ecuación es dada con decimales o con cantidades fraccionarias lo primero que debemos hacer es transformarla usando la multiplicación por una constante no nula para que nos deje solamente números enteros en las ecuaciones.
Al aplicar la formula Montante a la Matriz del Sistema de Ecuaciones hace transformaciones de esta para pasarla a otra Matriz Equivalente que tiene la misma solución que la original, hasta reducirla a un sistema que fácilmente se puede resolver. Las reglas a aplicar son las siguientes. Dado un Sistema de n Ecuaciones con n Incógnitas.
Reglas
- Se coloca la Matiz Aumentada
- Se toman n Pivotes (P.) tomando uno y solo uno de cada fila y columna de los coeficientes de las incógnitas. Se recomienda tomar los elementos de la Diagonal Principal como Pivotes.
- En cada transformación los elementos de fila del Pivote pasan iguales sin ser modificados.
- Los elementos de la columna del Pivote se convierten en “ceros” excepto el Pivote.
- Los “huecos” que queden en la nueva matriz serán llenados con la transformación de los elementos correspondientes de la matriz anterior mediante la aplicación de la formula Montante.
Apliquemos estas reglas a la solución de los siguientes:
Ejemplo

Solución
Escribiremos la Matriz Aumentada y aplicamos las reglas.

La ultima matriz representa al sistema de ecuaciones lineales equivalente:
Y su solución es:

Método de Faddev Leverrier
Sea A una matriz cuadrada cualquiera con ecuación característica:
![]()
Se representa con «trA» la traza de una matriz A y el método se expresa como:

De las ecuaciones recurrentes, se tiene:

Ejemplo

Solución
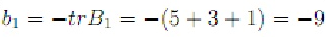





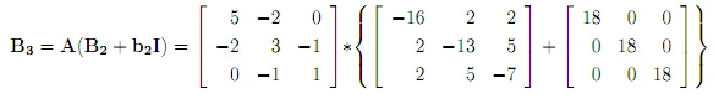

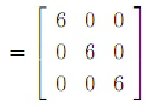
Por lo tanto la ecuación característica es:
![]()

